Propeller Balancing

I’ve always had a gear-driven alternator on the accessory case, but I recently added a belt-driven alternator. After relocating my RV-4 to a tower-controlled airport, I needed an alternator that could charge the battery while idling.

After installing the new alternator and having the propeller off the plane, I needed to rebalance the entire new assembly. I’ve always balanced my prop when it’s been off the plane or after being worked on or inspected. I would just pick the rpm and balance it following the instructions in the balancer’s manual. It usually took about three or four ground runs. However, like many of you, I never checked it at other rpm. I thought if it was balanced at 2400 rpm, it was good to go at all rpm.

Well, that’s just not so, and it’s why the balance manuals say to balance the prop at the rpm you run most of the time. So, why wasn’t it balanced at other rpm? Let’s take a deeper look at balancing and find out.

Why Balance?

Any severe out-of-balance condition will cause vibration leading to increased wear, fatigue of aircraft parts and occupant discomfort. There are three types of imbalances.

• Static imbalance is caused by one side of the propeller assembly being heavier than the other, which is everything in front of the crankshaft flange.
• Aerodynamic imbalance is caused by the difference in thrust of the different blades on the propeller.
• Coupling imbalance is caused by the combining of other rotating mass axes.

Static imbalance is when the center of mass isn’t concentric with the rotating center. In this case the phase angle is in one spot.

Aerodynamic imbalance is caused by one blade producing more thrust than another. The result is a kind of rotating wobble that might be due to different airfoils (repairs) or pitch variations between the blades on the prop. In this case, vibrational magnitude (measured in inches per second [IPS]) and phase angle change with rpm and prop load.

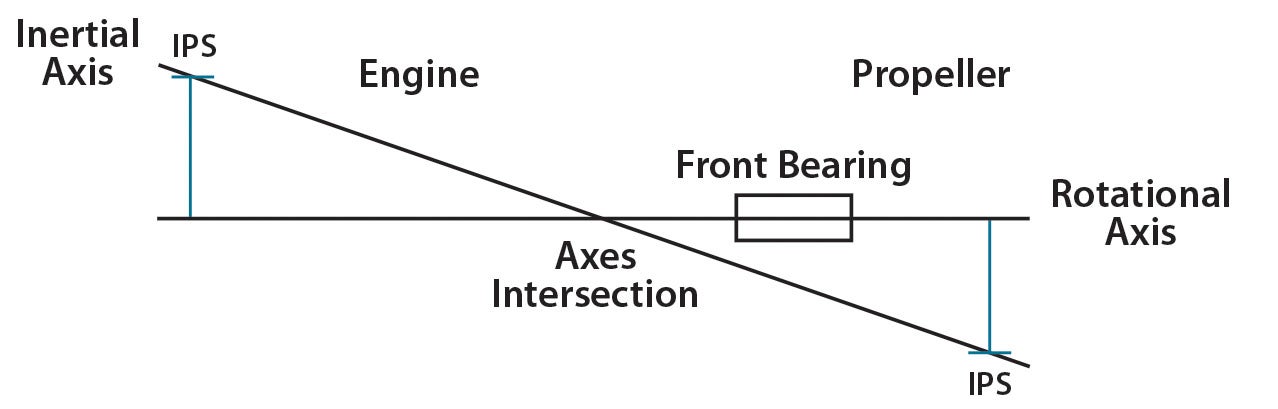
Coupling imbalance is when the rotational axis mass ahead of the front engine bearing is displaced from the inertial axis of the engine, which is behind the front engine bearing. These two axes intersect at the center of gravity along the crankshaft, but they are not parallel and concentric. In this case the phase angles in the front and back of the engine are 180° apart, but the IPS are the same, even though the rotating mass is dynamically balanced.

Coupling imbalance is the most difficult to understand and illustrate. It’s kind of a mass imbalance and an aerodynamic imbalance at the same time, but displaced along the rotational axis so they aren’t in the same plane.

As an aside, this is why some aircraft with certain engine/propeller combinations have rpm restrictions even though the engine/prop combination is balanced! It can be dangerous to operate continuously at coupling rpm ranges.

Then, to complicate things further, the propeller imbalance is composed of all of the mass imbalance, aerodynamic imbalances, and possibly a bit of coupling imbalances as well. And of these imbalances, the mass balance—if it is perfect—remains balanced at all rpm and the phase angle stays in the same location if the mass balance solution is in a single plane.

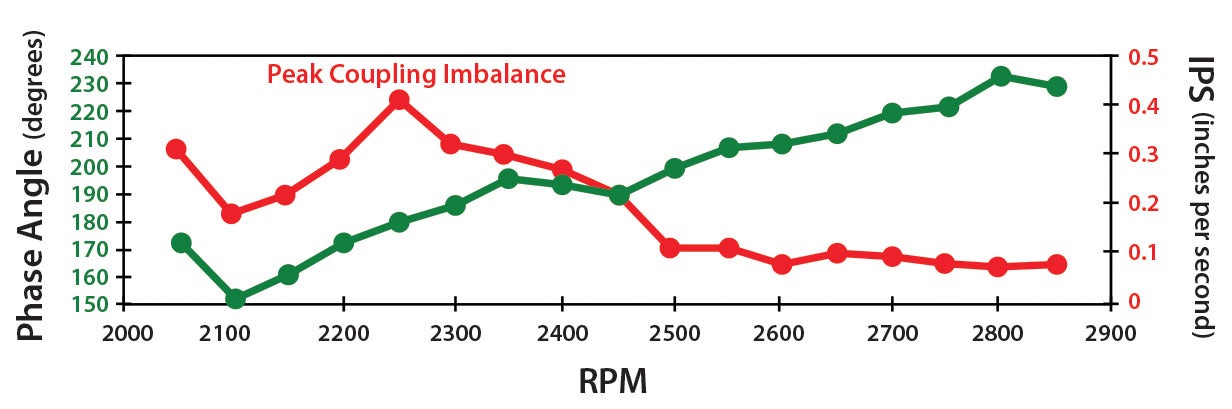
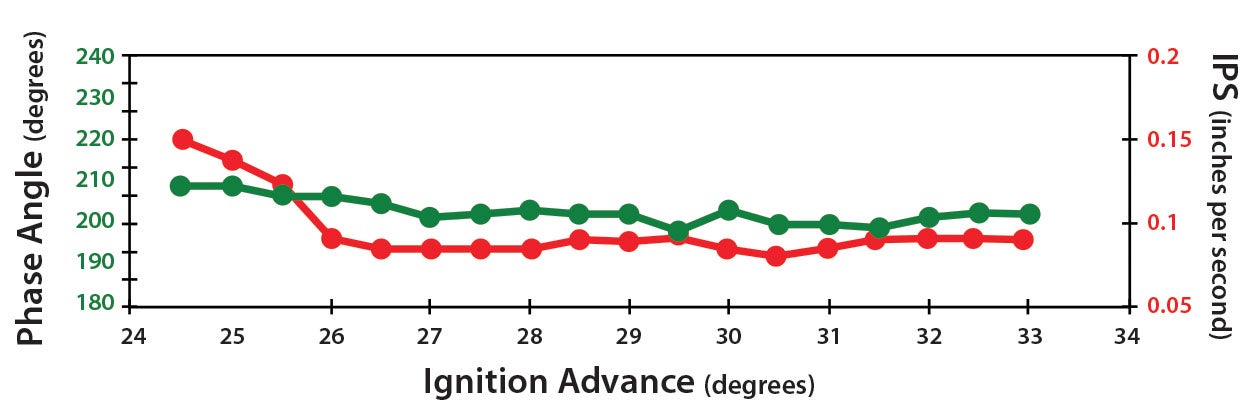
For dynamic imbalances, the IPS changes with the phase angle as load and rpm changes. Then you may also be running at the edges of the coupling imbalance range at times as well. (See the typical imbalance graph for rpm on Page 28. Every graph may/will vary with each plane’s individual propulsion system). It’s interesting to note that advancing the ignition timing decreased the IPS for the first 1.5° of advance, then had no effect at all on the remaining 7° of advance as the MAP decreased with increasing altitude, and there was essentially no effect on phase angle.

Balancers

There are a few on the market, with prices varying depending on available features. Of course, the more they do, the more they cost. One of the more popular models, and the one I use, is the DynaVibe Classic, which will do everything you need, costs less than many others and is simple to operate. The system uses a photo tachometer to provide rpm and location information via the light reflected from the reflective tape that goes on the back of the prop blade or flywheel. An accelerometer provides acceleration magnitude information to a handheld computer that produces a readout of rpm, IPS and phase angle on a screen.

All of the balancers available do essentially the same thing. They have the same or similar sensor accuracy, and all can produce acceptable results. Note that after balancing, even a few bugs can throw the balance off a little. If the bugs are asymmetric on the prop, they can cause mass and aerodynamic imbalances.

The difference in balancer cost doesn’t have as much to do with how accurate the balance ends up, but more with how much you want the balancer to do for you. The more complex units can diagnose engine problems, for example the magnitude of the coupling imbalance (with multiple sensors and locations on the engine). They can give you detailed information regarding the amount of corrective weight and its location, and divide that information into adjacent bolt locations on a starter ring. Some units also record the balance results for you. Just follow the manufacturer’s instructions, and you can end up with the results you want.

These balancers can be used on the ground or in flight, but the physical setup is the same idea. The mounts must be stiff, with the accelerometer as forward and as near the centerline of the engine case as possible, and the photo tachometer should be positioned perpendicularly to the back of the prop blade or flywheel. In-flight balancing, if you can do it, is very good on a smooth day and provides really reproducible data.

How to Balance Properly

The best advice is to follow the balancer’s manual! Balancing procedures aren’t difficult and can actually be fun.

Inspect the plane for things that can have an effect on the balance result. Needless to say, anything that holds the engine to the plane, is a rotating part on the engine, or is part of what is spinning must be in good condition; otherwise they can produce poor balancing results. Even an imbalanced alternator can produce vibrations.

The engine should be in good condition. If it is running rough, your results may be suboptimal.

The prop blades must track within acceptable limits. Just remove one set of spark plugs and use a dial indicator. The recommended limit is +/- 0.0625 inch. Mine is currently +/- 0.011 inch, which may be about average.

Test conditions have to be good with little wind or gusts. The balance manuals will define the test conditions for good balancing.

Be aware that certain aircraft will have an inherent disadvantage for ground-run balancing. For example, depending on the number of blades on the propeller, a taildragger with short landing gear will have two or three pulses per revolution that will input a vibration variable into the airframe every time the blade goes by the ground. This may, or may not, be a potential problem.

Pick a defined rpm (the one you run most of the time) and repeat the same rpm for sequential runs; do not let the rpm vary.

Correcting an Imbalance

There are only two things you have to find out to correct an imbalance at a specific rpm:

• Acceleration magnitude, measured in inches per second (IPS).
• Location, measured in degrees (phase angle).

Locate the position by phase angle, then add to the light spot or subtract from the heavy spot by adding or subtracting weights on the flywheel or spinner plate that equals the IPS. The balancer you use will have an easy formula to determine the amount of weight, and from the phase angle you can determine the location to add or subtract it. Just follow good techniques and proper procedures in the manual. It’s easy.

Here are other things that can affect balance and why you don’t want to vary them during the procedure.

• Gyroscopic precession causes the phase angle to shift into the direction of rotation of the propeller as the blade load increases. This is the principle that exists when a force is applied to a spinning object. It rotates into the direction of the object’s rotation and then reacts. So as the asymmetrical blade load increases, both the phase angle and IPS change.
• Changing rpm changes the centrifugal forces (IPS).
• Changing manifold pressure (MAP) changes the thrust loading on the blades. If they are uneven, it increases aerodynamic imbalance.

IPS

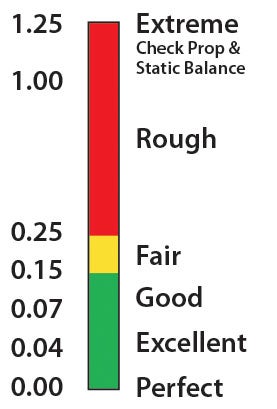
The lower the IPS (the acceleration magnitude of the imbalance in inches per second), the better for a good balance result. It is unlikely that you will notice much difference in the results between 0.07 IPS and 0.00 IPS. However, your airframe may notice over time with things like baffling cracking or rivets loosening. When getting a commercial balance, many providers will stop at around 0.10 IPS. As you get closer to 0.00, the phase angle can begin to be a variable, making it more difficult to put the weights in the proper location. And as you get closer to 0.00 IPS, the weight of the lightest bolt and nut may be too heavy for that location. Paul Dye had a very simple way to solve this problem by lightening the bolt and then adding titanium and aluminum bolts as alternatives (see “Hollow Bolts for Propeller Balancing“).

As you do consecutive runs, an IPS variability of around +/- 0.03 inch is essentially the same reading. If you’re doing in-flight data collection, you can easily take many consecutive readings, throw out the two extreme outliers, average the rest and you’ll get very good data.

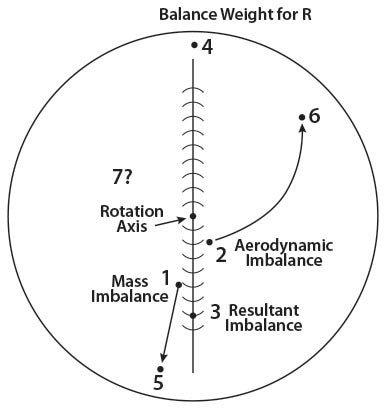
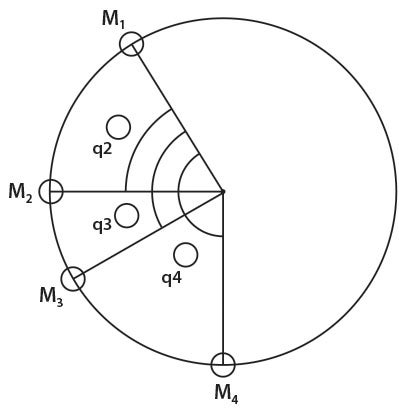
The IPS and phase angle can change as the rpm changes, and that’s why you balance at the rpm you use most of the time. The weight (R) at Position 4 in the graph above is the resultant weight that compensates for Position 1 and Position 2 imbalances at a specific rpm. If you observe the IPS and phase angles changing in value with changing rpm or MAP, you may be getting coupling and/or aerodynamic imbalance imposed on top of a rotating mass balance. The imbalances aren’t in the same spot in the rotating plane. The mass imbalance (1 in the diagram above) is in one spot (a single phase angle) relative to the central rotation axis and will only change IPS with increasing rpm. However, the aerodynamic imbalance (2 in the diagram) can change phase angle and IPS with increasing rpm as a result of increased MAP or pitch causing Position 2 to change toward Position 6 as prop load increases. So at the increased rpm it would require a totally new resultant solution for Position 7, wherever that may be. Balancing at all rpm is unlikely.

Aerodynamic imbalances are variable and can occur by just increasing MAP at the same rpm. In that case the mass imbalance (Position 1) wouldn’t increase, but the weight (4) to balance the R (resultant forces) would no longer be correct (7). Then throw in coupling, which is relative to the displacement of the rotational mass axis in respect to the engine’s inertial axis, and it can become complicated. If this is how complicated it is for constant-speed propellers, just think about how difficult it is to make a handmade propeller perfect.

If you are using a simple, inexpensive balancer, after a few runs you may end up with weights in a few locations instead of changing the weights and position each time you make a run. That’s OK, but if you want to reduce the location of weights on the flywheel or spinner to the minimum number, you could solve for the resultant (R) of several rotating masses in the same plane. Below is the space diagram for the analytical method.

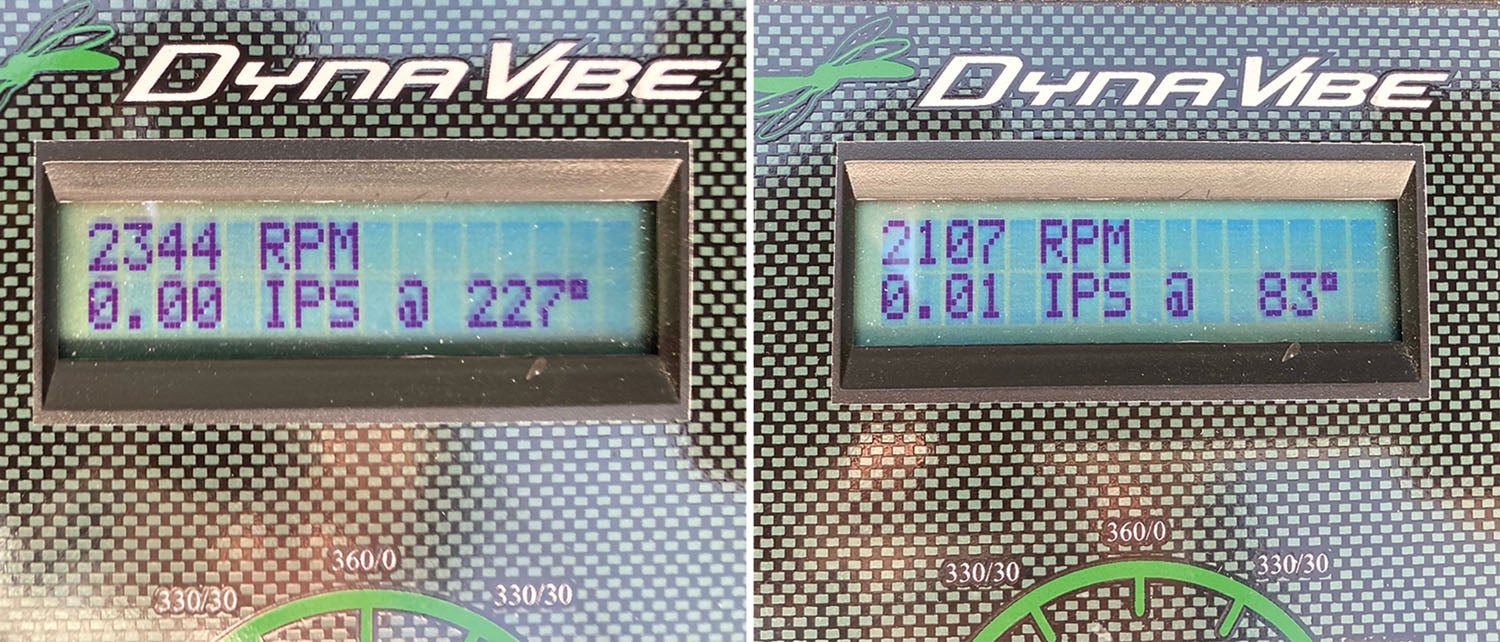
This was my plane after several in-flight runs as I was trying to find a good all-around balance resolution. I was testing at many different rpm that I like to use until I found an acceptable compromise for normal operations. The result was better than fair but not perfect. I also found an rpm range that I am not going to run anymore even though I have a counterweighted crank. The diagram below shows the solution for bolt locations on the Lycoming flywheel. Here is the math:

m = bolt weight in grams
r = radius of the flywheel bolt holes (5.375 inch on a Lycoming flywheel)
moment = m x r
q = angle in degrees from the reference, which is the first bolt position
R = resultant
H = horizontal component
V = vertical component

Weights (grams)		Angles (degrees from reference)
m1	8.8	q1	0 (reference)
m2	15.3	q2	60
m3	12.3	q3	90
m4	23.4	q4	150

Then solve for the horizontal component (moment arm) H.

H = moment₁ x Cos q₁ + moment₂ x Cos q₂ + moment₃ x Cos q₃ + moment₄ x Cosq₄

Right here, some of you are going, “What the heck…trigonometry?” But this is nothing. Just look up on your computer, “What is the cosine of 0,” and a calculator will pop up and solve things for you. What each component of the formula breaks down to is the following:

m₁ x r x cosine of q₁ = 8.5 x 5.375 x 1 = 45.6875

Now just put each value into the H equation:

H = 45.6875 + 41.1188 + 0 – 108.9243

H = -22.1180

Now solve V for the vertical component the same way as above.

V = moment₁ x Sin q₁ + moment₂ x Sin q₁ + moment₃ x Sin q₃ + moment₄ x Sin q₄

V = 200.2198

Then: the resultant R = the square root of ((H)² + (V)²)

R = 201.4376 g inches (moment in g inches)

Now: the moment (g inches)/r (inches) = m (g)

201.4376/5.375 inches = 37.48 g

This is the weight, but where does it go?

Tan of q = V/H = 201.4376 / -22.0657

q = Tan of -9.0657 (look up the tangent of -9.0657 on the computer)

q = 96.3 degrees from the reference q, which was 0° at m₁ position.

So 37.48 grams would go in the hole at 126.3° because the reference position was in the bolt hole position at 30° on the flywheel to begin with. Oh, but there’s no hole in that spot so we need two weights, with most of it in the 120° position and a little in the 150° position.

150–120 = 30° (distance the holes are apart).

6.3 is the number of degrees from the 120° hole.

6.3/30 = .21 (percentage of weight that needs to be in the bolt hole at 150°).

37.48 x .21 = 7.87 g goes in the 150° hole of the flywheel and 29.61 g goes in the 120° hole. However, this has the effect of reducing the arm of the moment by about 2.3%. So you could multiply the weights at both stations by 1.023 to get 30.29 g in the bolt hole at 120° and 8.05 g at 150°. But that’s only 0.86 g total, which would produce a very small change in final IPS, but knock yourself out if you want to do that math. It’s supposed to be fun.

If you’re persistent with in-flight balancing in smooth air, you can find the right weight and best position, then calculate it to a single- or double-weight location at the rpm that you most use. As you can see in the photos, I chose my low rpm cruise and my cruise climb rpm to dial in as close as possible. These two rpm avoid the peak coupling imbalance area. Remember, as you approach 0.00 IPS, the phase angle becomes more variable.

A Word to the Racers

If you are going to spend much time at very high rpm with tremendous prop loading, the only way to balance that is in flight under those same conditions. It most likely won’t be an acceptable weight balance solution for operating in normal conditions. Therefore, you need to carry your race balance solution (weights and locations) and change them for the race.

Acknowledgements

• RPX Technologies, manufacturer of DynaVibe Propeller Balancers
• Steve Sennett, RPX representative
• Jim Rust, Whirl Wind Propellers
• Trevor Parker, Hartzell Propeller, Inc.
• Knowledgeable Friends
  • Rich Jankowski, John Lynch and Klaus Savier